Detailed Description
A collection of functions to compute jacobians of diverse transformations, etc (some functions are redirections to existing methods elsewhere, so this namespace is actually used with grouping purposes).
Since most functions in this namespace are inline, their use implies no execution time overload and the code may be more clear to read, so it's recommended to use them where needed.
Functions | |
| void | jacob_quat_from_yawpitchroll (mrpt::math::CMatrixFixedNumeric< double, 4, 3 > &out_dq_dr, const double yaw, const double pitch, const double roll) |
| Computes the 4x3 Jacobian of the transformation from a 3D pose angles (yaw pitch roll) into a Quaternion, that is, the Jacobian of:
With : | |
| void | jacob_quat_from_yawpitchroll (mrpt::math::CMatrixFixedNumeric< double, 4, 3 > &out_dq_dr, const mrpt::poses::CPose3D &in_pose) |
| Computes the 4x3 Jacobian of the transformation from a 3D pose angles (yaw pitch roll) into a Quaternion, that is, the Jacobian of:
With : | |
| void | jacob_yawpitchroll_from_quat (mrpt::math::CMatrixFixedNumeric< double, 3, 4 > &out_dr_dq) |
| Computes the 3x4 Jacobian of the transformation from a quaternion (qr qx qy qz) to 3D pose angles (yaw pitch roll). More... | |
| template<class QUATERNION , class MATRIXLIKE > | |
| void | jacob_quat_rotation (const QUATERNION &quaternion, MATRIXLIKE &out_mat4x4) |
Compute the Jacobian of the rotation composition operation 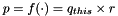 , that is the 4x4 matrix , that is the 4x4 matrix 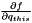 . More... . More... | |
| void | jacobs_6D_pose_comp (const mrpt::poses::CPose3D &x, const mrpt::poses::CPose3D &u, CMatrixDouble66 &out_df_dx, CMatrixDouble66 &out_df_du) |
Given the 3D(6D) pose composition 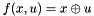 , compute the two 6x6 Jacobians , compute the two 6x6 Jacobians 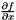 and and 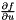 . More... . More... | |
| void | jacobs_6D_pose_comp (const mrpt::poses::CPose3DQuat &x, const mrpt::poses::CPose3DQuat &u, CMatrixDouble77 &out_df_dx, CMatrixDouble77 &out_df_du) |
Given the 3D(6D) pose composition 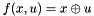 , compute the two 6x6 Jacobians , compute the two 6x6 Jacobians 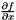 and and 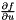 . More... . More... | |
| void | jacobs_2D_pose_comp (const mrpt::poses::CPosePDFGaussian &x, const mrpt::poses::CPosePDFGaussian &u, CMatrixDouble33 &out_df_dx, CMatrixDouble33 &out_df_du) |
Given the 2D pose composition 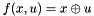 , compute the two 3x3 Jacobians , compute the two 3x3 Jacobians 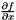 and and 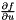 . More... . More... | |
| template<class VECTORLIKE , class VECTORLIKE2 , class VECTORLIKE3 , class MATRIXLIKE , class USERPARAM > | |
| void | jacob_numeric_estimate (const VECTORLIKE &x, void(*functor)(const VECTORLIKE &x, const USERPARAM &y, VECTORLIKE3 &out), const VECTORLIKE2 &increments, const USERPARAM &userParam, MATRIXLIKE &out_Jacobian) |
| Numerical estimation of the Jacobian of a user-supplied function - this template redirects to mrpt::math::estimateJacobian, see that function for documentation. More... | |
Function Documentation
◆ jacob_numeric_estimate()
|
inline |
Numerical estimation of the Jacobian of a user-supplied function - this template redirects to mrpt::math::estimateJacobian, see that function for documentation.
Definition at line 119 of file jacobians.h.
References mrpt::math::estimateJacobian().
Referenced by Pose3DTests::check_jacob_expe_e_at_0(), Pose3DTests::check_jacob_LnT_T(), mrpt::poses::CPose3DPDFGaussian::copyFrom(), mrpt::vision::recompute_errors_and_Jacobians(), Pose3DQuatTests::test_composePointJacob(), Pose3DTests::test_composePointJacob(), Pose3DTests::test_composePointJacob_se3(), Pose3DQuatTests::test_invComposePointJacob(), Pose3DTests::test_invComposePointJacob(), Pose3DTests::test_invComposePointJacob_se3(), Pose3DTests::test_Jacob_dAexpeD_de(), Pose3DTests::test_Jacob_dexpeD_de(), SE_traits_tests< POSE_TYPE >::test_jacobs_P1DP2inv(), Pose3DQuatTests::test_normalizeJacob(), Pose3DQuatTests::test_sphericalCoords(), Pose3DQuatPDFGaussTests::testCompositionJacobian(), Pose3DPDFGaussTests::testCompositionJacobian(), and mrpt::math::transform_gaussian_linear().
◆ jacob_quat_from_yawpitchroll() [1/2]
|
inline |
Computes the 4x3 Jacobian of the transformation from a 3D pose angles (yaw pitch roll) into a Quaternion, that is, the Jacobian of:
![\[ \mathbf{q} = \left( \begin{array}{c} \cos (\phi /2) \cos (\theta /2) \cos (\psi /2) + \sin (\phi /2) \sin (\theta /2) \sin (\psi /2) \\ \sin (\phi /2) \cos (\theta /2) \cos (\psi /2) - \cos (\phi /2) \sin (\theta /2) \sin (\psi /2) \\ \cos (\phi /2) \sin (\theta /2) \cos (\psi /2) + \sin (\phi /2) \cos (\theta /2) \sin (\psi /2) \\ \cos (\phi /2) \cos (\theta /2) \sin (\psi /2) - \sin (\phi /2) \sin (\theta /2) \cos (\psi /2) \\ \end{array}\right) \]](form_38.png)
With : 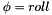 ,
, 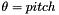 and
and 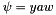 .
.
Definition at line 34 of file jacobians.h.
References mrpt::obs::gnss::pitch, mrpt::obs::gnss::roll, and mrpt::math::UNINITIALIZED_QUATERNION.
◆ jacob_quat_from_yawpitchroll() [2/2]
|
inline |
Computes the 4x3 Jacobian of the transformation from a 3D pose angles (yaw pitch roll) into a Quaternion, that is, the Jacobian of:
![\[ \mathbf{q} = \left( \begin{array}{c} \cos (\phi /2) \cos (\theta /2) \cos (\psi /2) + \sin (\phi /2) \sin (\theta /2) \sin (\psi /2) \\ \sin (\phi /2) \cos (\theta /2) \cos (\psi /2) - \cos (\phi /2) \sin (\theta /2) \sin (\psi /2) \\ \cos (\phi /2) \sin (\theta /2) \cos (\psi /2) + \sin (\phi /2) \cos (\theta /2) \sin (\psi /2) \\ \cos (\phi /2) \cos (\theta /2) \sin (\psi /2) - \sin (\phi /2) \sin (\theta /2) \cos (\psi /2) \\ \end{array}\right) \]](form_38.png)
With : 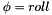 ,
, 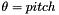 and
and 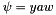 .
.
Definition at line 51 of file jacobians.h.
References mrpt::poses::CPose3D::getAsQuaternion(), and mrpt::math::UNINITIALIZED_QUATERNION.
◆ jacob_quat_rotation()
|
inline |
Compute the Jacobian of the rotation composition operation 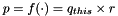 , that is the 4x4 matrix
, that is the 4x4 matrix 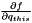 .
.
The output matrix can be a dynamic or fixed size (4x4) matrix. The input quaternion can be mrpt::math::CQuaternionFloat or mrpt::math::CQuaternionDouble.
Definition at line 76 of file jacobians.h.
◆ jacob_yawpitchroll_from_quat()
|
inline |
Computes the 3x4 Jacobian of the transformation from a quaternion (qr qx qy qz) to 3D pose angles (yaw pitch roll).
- See also
- jacob_quat_from_yawpitchroll
Definition at line 64 of file jacobians.h.
References MRPT_UNUSED_PARAM, and THROW_EXCEPTION.
◆ jacobs_2D_pose_comp()
|
inline |
Given the 2D pose composition 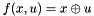 , compute the two 3x3 Jacobians
, compute the two 3x3 Jacobians 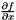 and
and 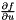 .
.
For the equations, see CPosePDF::jacobiansPoseComposition
Definition at line 108 of file jacobians.h.
References mrpt::poses::CPosePDF::jacobiansPoseComposition().
◆ jacobs_6D_pose_comp() [1/2]
|
inline |
Given the 3D(6D) pose composition 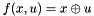 , compute the two 6x6 Jacobians
, compute the two 6x6 Jacobians 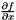 and
and 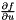 .
.
For the equations, see CPose3DPDF::jacobiansPoseComposition
Definition at line 84 of file jacobians.h.
References mrpt::poses::CPose3DPDF::jacobiansPoseComposition().
◆ jacobs_6D_pose_comp() [2/2]
|
inline |
Given the 3D(6D) pose composition 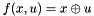 , compute the two 6x6 Jacobians
, compute the two 6x6 Jacobians 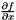 and
and 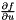 .
.
For the equations, see CPose3DQuatPDF::jacobiansPoseComposition
Definition at line 96 of file jacobians.h.
References mrpt::poses::CPose3DQuatPDF::jacobiansPoseComposition().