Detailed Description

|
Functions | |
| double BASE_IMPEXP | mrpt::math::normalPDF (double x, double mu, double std) |
| Evaluates the univariate normal (Gaussian) distribution at a given point "x". More... | |
| template<class VECTORLIKE1 , class VECTORLIKE2 , class MATRIXLIKE > | |
| MATRIXLIKE::Scalar | mrpt::math::normalPDFInf (const VECTORLIKE1 &x, const VECTORLIKE2 &mu, const MATRIXLIKE &cov_inv, const bool scaled_pdf=false) |
| Evaluates the multivariate normal (Gaussian) distribution at a given point "x". More... | |
| template<class VECTORLIKE1 , class VECTORLIKE2 , class MATRIXLIKE > | |
| MATRIXLIKE::Scalar | mrpt::math::normalPDF (const VECTORLIKE1 &x, const VECTORLIKE2 &mu, const MATRIXLIKE &cov, const bool scaled_pdf=false) |
| Evaluates the multivariate normal (Gaussian) distribution at a given point "x". More... | |
| template<typename VECTORLIKE , typename MATRIXLIKE > | |
| MATRIXLIKE::Scalar | mrpt::math::normalPDF (const VECTORLIKE &d, const MATRIXLIKE &cov) |
| Evaluates the multivariate normal (Gaussian) distribution at a given point given its distance vector "d" from the Gaussian mean. More... | |
| template<typename VECTORLIKE1 , typename MATRIXLIKE1 , typename VECTORLIKE2 , typename MATRIXLIKE2 > | |
| double | mrpt::math::KLD_Gaussians (const VECTORLIKE1 &mu0, const MATRIXLIKE1 &cov0, const VECTORLIKE2 &mu1, const MATRIXLIKE2 &cov1) |
| Kullback-Leibler divergence (KLD) between two independent multivariate Gaussians. More... | |
| double BASE_IMPEXP | mrpt::math::erfc (const double x) |
| The complementary error function of a Normal distribution. More... | |
| double BASE_IMPEXP | mrpt::math::erf (const double x) |
| The error function of a Normal distribution. More... | |
| double BASE_IMPEXP | mrpt::math::normalQuantile (double p) |
| Evaluates the Gaussian distribution quantile for the probability value p=[0,1]. More... | |
| double BASE_IMPEXP | mrpt::math::normalCDF (double p) |
| Evaluates the Gaussian cumulative density function. More... | |
| double BASE_IMPEXP | mrpt::math::chi2inv (double P, unsigned int dim=1) |
| The "quantile" of the Chi-Square distribution, for dimension "dim" and probability 0<P<1 (the inverse of chi2CDF) An aproximation from the Wilson-Hilferty transformation is used. More... | |
| double BASE_IMPEXP | mrpt::math::noncentralChi2CDF (unsigned int degreesOfFreedom, double noncentrality, double arg) |
| double BASE_IMPEXP | mrpt::math::chi2CDF (unsigned int degreesOfFreedom, double arg) |
| double BASE_IMPEXP | mrpt::math::chi2PDF (unsigned int degreesOfFreedom, double arg, double accuracy=1e-7) |
| std::pair< double, double > BASE_IMPEXP | mrpt::math::noncentralChi2PDF_CDF (unsigned int degreesOfFreedom, double noncentrality, double arg, double eps=1e-7) |
| Returns the 'exact' PDF (first) and CDF (second) of a Non-central chi-squared probability distribution, using an iterative method. More... | |
| template<typename CONTAINER > | |
| void | mrpt::math::confidenceIntervals (const CONTAINER &data, typename mrpt::math::ContainerType< CONTAINER >::element_t &out_mean, typename mrpt::math::ContainerType< CONTAINER >::element_t &out_lower_conf_interval, typename mrpt::math::ContainerType< CONTAINER >::element_t &out_upper_conf_interval, const double confidenceInterval=0.1, const size_t histogramNumBins=1000) |
| Return the mean and the 10%-90% confidence points (or with any other confidence value) of a set of samples by building the cummulative CDF of all the elements of the container. More... | |
| std::string BASE_IMPEXP | mrpt::math::MATLAB_plotCovariance2D (const CMatrixFloat &cov22, const CVectorFloat &mean, const float &stdCount, const std::string &style=std::string("b"), const size_t &nEllipsePoints=30) |
| Generates a string with the MATLAB commands required to plot an confidence interval (ellipse) for a 2D Gaussian ('float' version). More... | |
| std::string BASE_IMPEXP | mrpt::math::MATLAB_plotCovariance2D (const CMatrixDouble &cov22, const CVectorDouble &mean, const float &stdCount, const std::string &style=std::string("b"), const size_t &nEllipsePoints=30) |
| Generates a string with the MATLAB commands required to plot an confidence interval (ellipse) for a 2D Gaussian ('double' version). More... | |
Probability density distributions (pdf) distance metrics | |
| template<class VECTORLIKE1 , class VECTORLIKE2 , class MAT > | |
| MAT::Scalar | mrpt::math::mahalanobisDistance2 (const VECTORLIKE1 &X, const VECTORLIKE2 &MU, const MAT &COV) |
| Computes the squared mahalanobis distance of a vector X given the mean MU and the covariance inverse COV_inv
. More... | |
| template<class VECTORLIKE1 , class VECTORLIKE2 , class MAT > | |
| VECTORLIKE1::Scalar | mrpt::math::mahalanobisDistance (const VECTORLIKE1 &X, const VECTORLIKE2 &MU, const MAT &COV) |
| Computes the mahalanobis distance of a vector X given the mean MU and the covariance inverse COV_inv
. More... | |
| template<class VECTORLIKE , class MAT1 , class MAT2 , class MAT3 > | |
| MAT1::Scalar | mrpt::math::mahalanobisDistance2 (const VECTORLIKE &mean_diffs, const MAT1 &COV1, const MAT2 &COV2, const MAT3 &CROSS_COV12) |
| Computes the squared mahalanobis distance between two non-independent Gaussians, given the two covariance matrices and the vector with the difference of their means. More... | |
| template<class VECTORLIKE , class MAT1 , class MAT2 , class MAT3 > | |
| VECTORLIKE::Scalar | mrpt::math::mahalanobisDistance (const VECTORLIKE &mean_diffs, const MAT1 &COV1, const MAT2 &COV2, const MAT3 &CROSS_COV12) |
| Computes the mahalanobis distance between two non-independent Gaussians (or independent if CROSS_COV12=NULL), given the two covariance matrices and the vector with the difference of their means. More... | |
| template<class VECTORLIKE , class MATRIXLIKE > | |
| MATRIXLIKE::Scalar | mrpt::math::mahalanobisDistance2 (const VECTORLIKE &delta_mu, const MATRIXLIKE &cov) |
| Computes the squared mahalanobis distance between a point and a Gaussian, given the covariance matrix and the vector with the difference between the mean and the point. More... | |
| template<class VECTORLIKE , class MATRIXLIKE > | |
| MATRIXLIKE::Scalar | mrpt::math::mahalanobisDistance (const VECTORLIKE &delta_mu, const MATRIXLIKE &cov) |
| Computes the mahalanobis distance between a point and a Gaussian, given the covariance matrix and the vector with the difference between the mean and the point. More... | |
| template<typename T > | |
| T | mrpt::math::productIntegralTwoGaussians (const std::vector< T > &mean_diffs, const CMatrixTemplateNumeric< T > &COV1, const CMatrixTemplateNumeric< T > &COV2) |
| Computes the integral of the product of two Gaussians, with means separated by "mean_diffs" and covariances "COV1" and "COV2". More... | |
| template<typename T , size_t DIM> | |
| T | mrpt::math::productIntegralTwoGaussians (const std::vector< T > &mean_diffs, const CMatrixFixedNumeric< T, DIM, DIM > &COV1, const CMatrixFixedNumeric< T, DIM, DIM > &COV2) |
| Computes the integral of the product of two Gaussians, with means separated by "mean_diffs" and covariances "COV1" and "COV2". More... | |
| template<typename T , class VECLIKE , class MATLIKE1 , class MATLIKE2 > | |
| void | mrpt::math::productIntegralAndMahalanobisTwoGaussians (const VECLIKE &mean_diffs, const MATLIKE1 &COV1, const MATLIKE2 &COV2, T &maha2_out, T &intprod_out, const MATLIKE1 *CROSS_COV12=NULL) |
| Computes both, the integral of the product of two Gaussians and their square Mahalanobis distance. More... | |
| template<typename T , class VECLIKE , class MATRIXLIKE > | |
| void | mrpt::math::mahalanobisDistance2AndLogPDF (const VECLIKE &diff_mean, const MATRIXLIKE &cov, T &maha2_out, T &log_pdf_out) |
| Computes both, the logarithm of the PDF and the square Mahalanobis distance between a point (given by its difference wrt the mean) and a Gaussian. More... | |
| template<typename T , class VECLIKE , class MATRIXLIKE > | |
| void | mrpt::math::mahalanobisDistance2AndPDF (const VECLIKE &diff_mean, const MATRIXLIKE &cov, T &maha2_out, T &pdf_out) |
| Computes both, the PDF and the square Mahalanobis distance between a point (given by its difference wrt the mean) and a Gaussian. More... | |
| template<class VECTOR_OF_VECTORS , class MATRIXLIKE , class VECTORLIKE , class VECTORLIKE2 , class VECTORLIKE3 > | |
| void | mrpt::math::covariancesAndMeanWeighted (const VECTOR_OF_VECTORS &elements, MATRIXLIKE &covariances, VECTORLIKE &means, const VECTORLIKE2 *weights_mean, const VECTORLIKE3 *weights_cov, const bool *elem_do_wrap2pi=NULL) |
| Computes covariances and mean of any vector of containers, given optional weights for the different samples. More... | |
| template<class VECTOR_OF_VECTORS , class MATRIXLIKE , class VECTORLIKE > | |
| void | mrpt::math::covariancesAndMean (const VECTOR_OF_VECTORS &elements, MATRIXLIKE &covariances, VECTORLIKE &means, const bool *elem_do_wrap2pi=NULL) |
| Computes covariances and mean of any vector of containers. More... | |
| template<class VECTORLIKE1 , class VECTORLIKE2 > | |
| void | mrpt::math::weightedHistogram (const VECTORLIKE1 &values, const VECTORLIKE1 &weights, float binWidth, VECTORLIKE2 &out_binCenters, VECTORLIKE2 &out_binValues) |
| Computes the weighted histogram for a vector of values and their corresponding weights. More... | |
| template<class VECTORLIKE1 , class VECTORLIKE2 > | |
| void | mrpt::math::weightedHistogramLog (const VECTORLIKE1 &values, const VECTORLIKE1 &log_weights, float binWidth, VECTORLIKE2 &out_binCenters, VECTORLIKE2 &out_binValues) |
| Computes the weighted histogram for a vector of values and their corresponding log-weights. More... | |
| double BASE_IMPEXP | mrpt::math::averageLogLikelihood (const CVectorDouble &logLikelihoods) |
| A numerically-stable method to compute average likelihood values with strongly different ranges (unweighted likelihoods: compute the arithmetic mean). More... | |
| double BASE_IMPEXP | mrpt::math::averageWrap2Pi (const CVectorDouble &angles) |
Computes the average of a sequence of angles in radians taking into account the correct wrapping in the range ![$ ]-\pi,\pi [ $](form_24.png) , for example, the mean of (2,-2) is , for example, the mean of (2,-2) is 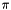 , not 0. More... , not 0. More... | |
| double BASE_IMPEXP | mrpt::math::averageLogLikelihood (const CVectorDouble &logWeights, const CVectorDouble &logLikelihoods) |
| A numerically-stable method to average likelihood values with strongly different ranges (weighted likelihoods). More... | |
Function Documentation
◆ averageLogLikelihood() [1/2]
| double mrpt::math::averageLogLikelihood | ( | const CVectorDouble & | logLikelihoods | ) |
A numerically-stable method to compute average likelihood values with strongly different ranges (unweighted likelihoods: compute the arithmetic mean).
This method implements this equation:
![\[ return = - \log N + \log \sum_{i=1}^N e^{ll_i-ll_{max}} + ll_{max} \]](form_23.png)
See also the tutorial page.
Definition at line 1840 of file math.cpp.
References mrpt::math::maximum(), MRPT_CHECK_NORMAL_NUMBER, MRPT_END, MRPT_START, and THROW_EXCEPTION.
Referenced by mrpt::maps::CBeaconMap::internal_computeObservationLikelihood(), mrpt::slam::PF_implementation< mrpt::poses::CPose3D, CMonteCarloLocalization3D >::PF_SLAM_particlesEvaluator_AuxPFOptimal(), and mrpt::slam::PF_implementation< mrpt::poses::CPose3D, CMonteCarloLocalization3D >::PF_SLAM_particlesEvaluator_AuxPFStandard().
◆ averageLogLikelihood() [2/2]
| double mrpt::math::averageLogLikelihood | ( | const CVectorDouble & | logWeights, |
| const CVectorDouble & | logLikelihoods | ||
| ) |
A numerically-stable method to average likelihood values with strongly different ranges (weighted likelihoods).
This method implements this equation:
![\[ return = \log \left( \frac{1}{\sum_i e^{lw_i}} \sum_i e^{lw_i} e^{ll_i} \right) \]](form_26.png)
See also the tutorial page.
Definition at line 1808 of file math.cpp.
References ASSERT_, mrpt::math::maximum(), MRPT_CHECK_NORMAL_NUMBER, MRPT_END, MRPT_START, and THROW_EXCEPTION.
◆ averageWrap2Pi()
| double mrpt::math::averageWrap2Pi | ( | const CVectorDouble & | angles | ) |
Computes the average of a sequence of angles in radians taking into account the correct wrapping in the range ![$ ]-\pi,\pi [ $](form_24.png) , for example, the mean of (2,-2) is
, for example, the mean of (2,-2) is 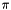 , not 0.
, not 0.
Definition at line 1864 of file math.cpp.
Referenced by mrpt::topography::path_from_rtk_gps().
◆ chi2CDF()
| double mrpt::mrpt::math::chi2CDF | ( | unsigned int | degreesOfFreedom, |
| double | arg | ||
| ) |
Cumulative chi square distribution.
Computes the cumulative density of a chi square distribution with \a degreesOfFreedom and tolerance \a accuracy at the given argument \a arg, i.e. the probability that a random number drawn from the distribution is below \a arg by calling <tt>noncentralChi2CDF(degreesOfFreedom, 0.0, arg, accuracy)</tt>. \note Function code from the Vigra project (http://hci.iwr.uni-heidelberg.de/vigra/); code under "MIT X11 License", GNU GPL-compatible.
Definition at line 2098 of file math.cpp.
References mrpt::math::noncentralChi2CDF().
◆ chi2inv()
| double mrpt::math::chi2inv | ( | double | P, |
| unsigned int | dim = 1 |
||
| ) |
The "quantile" of the Chi-Square distribution, for dimension "dim" and probability 0<P<1 (the inverse of chi2CDF) An aproximation from the Wilson-Hilferty transformation is used.
- Note
- Equivalent to MATLAB chi2inv(), but note that this is just an approximation, which becomes very poor for small values of "P".
Definition at line 967 of file math.cpp.
References ASSERT_, and mrpt::math::normalQuantile().
Referenced by mrpt::slam::CGridMapAligner::AlignPDF_robustMatch(), mrpt::slam::data_association_full_covariance(), mrpt::hmtslam::CHMTSLAM::LSLAM_process_message_from_TBI(), mrpt::slam::PF_implementation< mrpt::poses::CPose3D, CMonteCarloLocalization3D >::PF_SLAM_implementation_pfAuxiliaryPFStandardAndOptimal(), mrpt::slam::PF_implementation< mrpt::poses::CPose3D, CMonteCarloLocalization3D >::PF_SLAM_implementation_pfStandardProposal(), mrpt::tfest::se2_l2_robust(), and TEST().
◆ chi2PDF()
| double mrpt::mrpt::math::chi2PDF | ( | unsigned int | degreesOfFreedom, |
| double | arg, | ||
| double | accuracy = 1e-7 |
||
| ) |
Chi square distribution PDF. Computes the density of a chi square distribution with degreesOfFreedom and tolerance accuracy at the given argument arg by calling noncentralChi2(degreesOfFreedom, 0.0, arg, accuracy).
- Note
- Function code from the Vigra project (http://hci.iwr.uni-heidelberg.de/vigra/); code under "MIT X11 License", GNU GPL-compatible.
- Equivalent to MATLAB's chi2pdf(arg,degreesOfFreedom)
Definition at line 2189 of file math.cpp.
References mrpt::math::noncentralChi2PDF_CDF().
Referenced by TEST().
◆ confidenceIntervals()
| void mrpt::math::confidenceIntervals | ( | const CONTAINER & | data, |
| typename mrpt::math::ContainerType< CONTAINER >::element_t & | out_mean, | ||
| typename mrpt::math::ContainerType< CONTAINER >::element_t & | out_lower_conf_interval, | ||
| typename mrpt::math::ContainerType< CONTAINER >::element_t & | out_upper_conf_interval, | ||
| const double | confidenceInterval = 0.1, |
||
| const size_t | histogramNumBins = 1000 |
||
| ) |
Return the mean and the 10%-90% confidence points (or with any other confidence value) of a set of samples by building the cummulative CDF of all the elements of the container.
The container can be any MRPT container (CArray, matrices, vectors).
- Parameters
-
confidenceInterval A number in the range (0,1) such as the confidence interval will be [100*confidenceInterval, 100*(1-confidenceInterval)].
Definition at line 184 of file distributions.h.
References ASSERT_, mrpt::math::cumsum(), mrpt::math::distance(), mrpt::math::histogram(), mrpt::math::maximum(), mrpt::math::mean(), mrpt::math::minimum_maximum(), MRPT_END, and MRPT_START.
◆ covariancesAndMean()
| void mrpt::math::covariancesAndMean | ( | const VECTOR_OF_VECTORS & | elements, |
| MATRIXLIKE & | covariances, | ||
| VECTORLIKE & | means, | ||
| const bool * | elem_do_wrap2pi = NULL |
||
| ) |
Computes covariances and mean of any vector of containers.
- Parameters
-
elements Any kind of vector of vectors/arrays, eg. std::vector<mrpt::math::CVectorDouble>, with all the input samples, each sample in a "row". covariances Output estimated covariance; it can be a fixed/dynamic matrix or a matrixview. means Output estimated mean; it can be CVectorDouble/CArrayDouble, etc... elem_do_wrap2pi If !=NULL; it must point to an array of "bool" of size()==dimension of each element, stating if it's needed to do a wrap to [-pi,pi] to each dimension.
Definition at line 354 of file data_utils.h.
Referenced by mrpt::math::getRegressionLine(), mrpt::math::getRegressionPlane(), and mrpt::math::transform_gaussian_montecarlo().
◆ covariancesAndMeanWeighted()
|
inline |
Computes covariances and mean of any vector of containers, given optional weights for the different samples.
- Parameters
-
elements Any kind of vector of vectors/arrays, eg. std::vector<mrpt::math::CVectorDouble>, with all the input samples, each sample in a "row". covariances Output estimated covariance; it can be a fixed/dynamic matrix or a matrixview. means Output estimated mean; it can be CVectorDouble/CArrayDouble, etc... weights_mean If !=NULL, it must point to a vector of size()==number of elements, with normalized weights to take into account for the mean. weights_cov If !=NULL, it must point to a vector of size()==number of elements, with normalized weights to take into account for the covariance. elem_do_wrap2pi If !=NULL; it must point to an array of "bool" of size()==dimension of each element, stating if it's needed to do a wrap to [-pi,pi] to each dimension.
- See also
- This method is used in mrpt::math::unscented_transform_gaussian
Definition at line 251 of file data_utils.h.
References ASSERTDEB_, ASSERTMSG_, M_2PI, M_PI, and mrpt::math::wrapToPi().
Referenced by mrpt::math::transform_gaussian_unscented().
◆ erf()
| double mrpt::math::erf | ( | const double | x | ) |
The error function of a Normal distribution.
Definition at line 955 of file math.cpp.
References mrpt::math::erfc().
Referenced by mrpt::math::noncentralChi2CDF(), mrpt::math::noncentralChi2PDF_CDF(), and TEST().
◆ erfc()
| double mrpt::math::erfc | ( | const double | x | ) |
The complementary error function of a Normal distribution.
Definition at line 917 of file math.cpp.
References mrpt::obs::gnss::a1, mrpt::obs::gnss::a2, and mrpt::obs::gnss::a3.
Referenced by mrpt::math::erf(), and TEST().
◆ KLD_Gaussians()
| double mrpt::math::KLD_Gaussians | ( | const VECTORLIKE1 & | mu0, |
| const MATRIXLIKE1 & | cov0, | ||
| const VECTORLIKE2 & | mu1, | ||
| const MATRIXLIKE2 & | cov1 | ||
| ) |
Kullback-Leibler divergence (KLD) between two independent multivariate Gaussians.
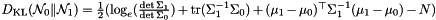
Definition at line 96 of file distributions.h.
References ASSERT_, MRPT_END, MRPT_START, mrpt::math::multiply_HCHt_scalar(), and mrpt::math::size().
◆ mahalanobisDistance() [1/3]
|
inline |
Computes the mahalanobis distance of a vector X given the mean MU and the covariance inverse COV_inv
![\[ d = \sqrt{ (X-MU)^\top \Sigma^{-1} (X-MU) } \]](form_16.png)
.
Definition at line 58 of file data_utils.h.
References mrpt::math::mahalanobisDistance2().
Referenced by mrpt::math::mahalanobisDistance(), mrpt::poses::CPose3DQuatPDFGaussian::mahalanobisDistanceTo(), and mrpt::topography::path_from_rtk_gps().
◆ mahalanobisDistance() [2/3]
|
inline |
Computes the mahalanobis distance between two non-independent Gaussians (or independent if CROSS_COV12=NULL), given the two covariance matrices and the vector with the difference of their means.
![\[ d = \sqrt{ \Delta_\mu^\top (\Sigma_1 + \Sigma_2 - 2 \Sigma_12 )^{-1} \Delta_\mu } \]](form_18.png)
Definition at line 98 of file data_utils.h.
References mrpt::math::mahalanobisDistance().
◆ mahalanobisDistance() [3/3]
|
inline |
Computes the mahalanobis distance between a point and a Gaussian, given the covariance matrix and the vector with the difference between the mean and the point.
![\[ d^2 = \sqrt( \Delta_\mu^\top \Sigma^{-1} \Delta_\mu ) \]](form_20.png)
Definition at line 124 of file data_utils.h.
References mrpt::math::cov(), and mrpt::math::mahalanobisDistance2().
◆ mahalanobisDistance2() [1/3]
| MAT::Scalar mrpt::math::mahalanobisDistance2 | ( | const VECTORLIKE1 & | X, |
| const VECTORLIKE2 & | MU, | ||
| const MAT & | COV | ||
| ) |
Computes the squared mahalanobis distance of a vector X given the mean MU and the covariance inverse COV_inv
![\[ d^2 = (X-MU)^\top \Sigma^{-1} (X-MU) \]](form_15.png)
.
Definition at line 34 of file data_utils.h.
References ASSERT_, MRPT_END, MRPT_START, and mrpt::math::size().
Referenced by mrpt::math::mahalanobisDistance(), and mrpt::graphslam::deciders::CLoopCloserERD< GRAPH_T >::mahalanobisDistanceOdometryToICPEdge().
◆ mahalanobisDistance2() [2/3]
| MAT1::Scalar mrpt::math::mahalanobisDistance2 | ( | const VECTORLIKE & | mean_diffs, |
| const MAT1 & | COV1, | ||
| const MAT2 & | COV2, | ||
| const MAT3 & | CROSS_COV12 | ||
| ) |
Computes the squared mahalanobis distance between two non-independent Gaussians, given the two covariance matrices and the vector with the difference of their means.
![\[ d^2 = \Delta_\mu^\top (\Sigma_1 + \Sigma_2 - 2 \Sigma_12 )^{-1} \Delta_\mu \]](form_17.png)
Definition at line 72 of file data_utils.h.
References ASSERT_, MRPT_END, MRPT_START, mrpt::math::multiply_HCHt_scalar(), and mrpt::math::size().
◆ mahalanobisDistance2() [3/3]
|
inline |
Computes the squared mahalanobis distance between a point and a Gaussian, given the covariance matrix and the vector with the difference between the mean and the point.
![\[ d^2 = \Delta_\mu^\top \Sigma^{-1} \Delta_\mu \]](form_19.png)
Definition at line 112 of file data_utils.h.
References ASSERTDEB_, mrpt::math::cov(), and mrpt::math::multiply_HCHt_scalar().
◆ mahalanobisDistance2AndLogPDF()
| void mrpt::math::mahalanobisDistance2AndLogPDF | ( | const VECLIKE & | diff_mean, |
| const MATRIXLIKE & | cov, | ||
| T & | maha2_out, | ||
| T & | log_pdf_out | ||
| ) |
Computes both, the logarithm of the PDF and the square Mahalanobis distance between a point (given by its difference wrt the mean) and a Gaussian.
Definition at line 205 of file data_utils.h.
References ASSERTDEB_, mrpt::math::cov(), M_2PI, MRPT_END, MRPT_START, and mrpt::math::multiply_HCHt_scalar().
Referenced by mrpt::slam::data_association_full_covariance(), mrpt::math::mahalanobisDistance2AndPDF(), and mrpt::slam::CRangeBearingKFSLAM2D::OnGetObservationsAndDataAssociation().
◆ mahalanobisDistance2AndPDF()
|
inline |
Computes both, the PDF and the square Mahalanobis distance between a point (given by its difference wrt the mean) and a Gaussian.
Definition at line 229 of file data_utils.h.
References mrpt::math::cov(), and mrpt::math::mahalanobisDistance2AndLogPDF().
◆ MATLAB_plotCovariance2D() [1/2]
| string mrpt::math::MATLAB_plotCovariance2D | ( | const CMatrixFloat & | cov22, |
| const CVectorFloat & | mean, | ||
| const float & | stdCount, | ||
| const std::string & | style = std::string("b"), |
||
| const size_t & | nEllipsePoints = 30 |
||
| ) |
Generates a string with the MATLAB commands required to plot an confidence interval (ellipse) for a 2D Gaussian ('float' version).
- Parameters
-
cov22 The 2x2 covariance matrix mean The 2-length vector with the mean stdCount How many "quantiles" to get into the area of the ellipse: 2: 95%, 3:99.97%,... style A matlab style string, for colors, line styles,... nEllipsePoints The number of points in the ellipse to generate
Definition at line 1905 of file math.cpp.
References mrpt::math::cov(), mean(), MRPT_END, and MRPT_START.
Referenced by mrpt::slam::CRangeBearingKFSLAM2D::saveMapAndPath2DRepresentationAsMATLABFile(), and mrpt::slam::CRangeBearingKFSLAM::saveMapAndPath2DRepresentationAsMATLABFile().
◆ MATLAB_plotCovariance2D() [2/2]
| string mrpt::math::MATLAB_plotCovariance2D | ( | const CMatrixDouble & | cov22, |
| const CVectorDouble & | mean, | ||
| const float & | stdCount, | ||
| const std::string & | style = std::string("b"), |
||
| const size_t & | nEllipsePoints = 30 |
||
| ) |
Generates a string with the MATLAB commands required to plot an confidence interval (ellipse) for a 2D Gaussian ('double' version).
- Parameters
-
cov22 The 2x2 covariance matrix mean The 2-length vector with the mean stdCount How many "quantiles" to get into the area of the ellipse: 2: 95%, 3:99.97%,... style A matlab style string, for colors, line styles,... nEllipsePoints The number of points in the ellipse to generate
Definition at line 1923 of file math.cpp.
References ASSERT_, mrpt::math::cov(), mrpt::format(), M_2PI, mean(), MRPT_END_WITH_CLEAN_UP, and MRPT_START.
◆ noncentralChi2CDF()
| double mrpt::mrpt::math::noncentralChi2CDF | ( | unsigned int | degreesOfFreedom, |
| double | noncentrality, | ||
| double | arg | ||
| ) |
Cumulative non-central chi square distribution (approximate).
Computes approximate values of the cumulative density of a chi square distribution with \a degreesOfFreedom, and noncentrality parameter \a noncentrality at the given argument \a arg, i.e. the probability that a random number drawn from the distribution is below \a arg It uses the approximate transform into a normal distribution due to Wilson and Hilferty (see Abramovitz, Stegun: "Handbook of Mathematical Functions", formula 26.3.32). The algorithm's running time is independent of the inputs. The accuracy is only about 0.1 for few degrees of freedom, but reaches about 0.001 above dof = 5. \note Function code from the Vigra project (http://hci.iwr.uni-heidelberg.de/vigra/); code under "MIT X11 License", GNU GPL-compatible.
- See also
- noncentralChi2PDF_CDF
Definition at line 2194 of file math.cpp.
References mrpt::math::erf(), and mrpt::math::square().
Referenced by mrpt::math::chi2CDF().
◆ noncentralChi2PDF_CDF()
| std::pair< double, double > mrpt::mrpt::math::noncentralChi2PDF_CDF | ( | unsigned int | degreesOfFreedom, |
| double | noncentrality, | ||
| double | arg, | ||
| double | eps = 1e-7 |
||
| ) |
Returns the 'exact' PDF (first) and CDF (second) of a Non-central chi-squared probability distribution, using an iterative method.
- Note
- Equivalent to MATLAB's ncx2cdf(arg,degreesOfFreedom,noncentrality)
Definition at line 2120 of file math.cpp.
References ASSERTMSG_, mrpt::obs::gnss::b1, eps, mrpt::math::erf(), min, noncentralChi2OneIteration(), mrpt::math::sum(), and THROW_EXCEPTION.
Referenced by mrpt::math::chi2PDF(), and TEST().
◆ normalCDF()
| double mrpt::math::normalCDF | ( | double | p | ) |
Evaluates the Gaussian cumulative density function.
The employed approximation is that from W. J. Cody freely available in http://www.netlib.org/specfun/erf
- Note
- Equivalent to MATLAB normcdf(x,mu,s) with p=(x-mu)/s
Definition at line 1108 of file math.cpp.
References ASSERT_, mrpt::math::isFinite(), and mrpt::math::isNaN().
Referenced by mrpt::math::normalQuantile(), and TEST().
◆ normalPDF() [1/3]
| double mrpt::math::normalPDF | ( | double | x, |
| double | mu, | ||
| double | std | ||
| ) |
Evaluates the univariate normal (Gaussian) distribution at a given point "x".
Definition at line 908 of file math.cpp.
References mrpt::math::square().
Referenced by mrpt::poses::CPose3DQuatPDFGaussian::evaluateNormalizedPDF(), mrpt::poses::CPosePDFGaussianInf::evaluateNormalizedPDF(), mrpt::poses::CPosePDFGaussian::evaluateNormalizedPDF(), mrpt::poses::CPosePDFSOG::evaluateNormalizedPDF(), mrpt::poses::CPose3DQuatPDFGaussian::evaluatePDF(), mrpt::poses::CPosePDFGaussianInf::evaluatePDF(), mrpt::poses::CPosePDFGaussian::evaluatePDF(), mrpt::poses::CPosePDFSOG::evaluatePDF(), mrpt::poses::CPointPDFSOG::evaluatePDF(), mrpt::poses::CPosePDFParticles::evaluatePDF_parzen(), and TEST().
◆ normalPDF() [2/3]
|
inline |
Evaluates the multivariate normal (Gaussian) distribution at a given point "x".
- Parameters
-
x A vector or column or row matrix with the point at which to evaluate the pdf. mu A vector or column or row matrix with the Gaussian mean. cov The covariance matrix of the Gaussian. scaled_pdf If set to true, the PDF will be scaled to be in the range [0,1], in contrast to its integral from [-inf,+inf] being 1.
Definition at line 65 of file distributions.h.
References mrpt::math::cov(), and mrpt::math::normalPDFInf().
◆ normalPDF() [3/3]
| MATRIXLIKE::Scalar mrpt::math::normalPDF | ( | const VECTORLIKE & | d, |
| const MATRIXLIKE & | cov | ||
| ) |
Evaluates the multivariate normal (Gaussian) distribution at a given point given its distance vector "d" from the Gaussian mean.
Definition at line 78 of file distributions.h.
References ASSERTDEB_, mrpt::math::cov(), M_2PI, MRPT_END, MRPT_START, and mrpt::math::multiply_HCHt_scalar().
◆ normalPDFInf()
|
inline |
Evaluates the multivariate normal (Gaussian) distribution at a given point "x".
- Parameters
-
x A vector or column or row matrix with the point at which to evaluate the pdf. mu A vector or column or row matrix with the Gaussian mean. cov_inv The inverse covariance (information) matrix of the Gaussian. scaled_pdf If set to true, the PDF will be scaled to be in the range [0,1], in contrast to its integral from [-inf,+inf] being 1.
Definition at line 42 of file distributions.h.
References ASSERTDEB_, M_2PI, MRPT_END, MRPT_START, mrpt::math::multiply_HCHt_scalar(), and mrpt::math::size().
Referenced by mrpt::poses::CPose3DQuatPDFGaussianInf::evaluateNormalizedPDF(), mrpt::poses::CPose3DQuatPDFGaussianInf::evaluatePDF(), and mrpt::math::normalPDF().
◆ normalQuantile()
| double mrpt::math::normalQuantile | ( | double | p | ) |
Evaluates the Gaussian distribution quantile for the probability value p=[0,1].
The employed approximation is that from Peter J. Acklam (pjacklam@online.no), freely available in http://home.online.no/~pjacklam.
Definition at line 1046 of file math.cpp.
References ASSERT_, mrpt::math::isNaN(), min, and mrpt::math::normalCDF().
Referenced by mrpt::math::chi2inv().
◆ productIntegralAndMahalanobisTwoGaussians()
| void mrpt::math::productIntegralAndMahalanobisTwoGaussians | ( | const VECLIKE & | mean_diffs, |
| const MATLIKE1 & | COV1, | ||
| const MATLIKE2 & | COV2, | ||
| T & | maha2_out, | ||
| T & | intprod_out, | ||
| const MATLIKE1 * | CROSS_COV12 = NULL |
||
| ) |
Computes both, the integral of the product of two Gaussians and their square Mahalanobis distance.
Definition at line 178 of file data_utils.h.
◆ productIntegralTwoGaussians() [1/2]
| T mrpt::math::productIntegralTwoGaussians | ( | const std::vector< T > & | mean_diffs, |
| const CMatrixTemplateNumeric< T > & | COV1, | ||
| const CMatrixTemplateNumeric< T > & | COV2 | ||
| ) |
Computes the integral of the product of two Gaussians, with means separated by "mean_diffs" and covariances "COV1" and "COV2".
![\[ D = \frac{1}{(2 \pi)^{0.5 N} \sqrt{} } \exp( \Delta_\mu^\top (\Sigma_1 + \Sigma_2 - 2 \Sigma_12)^{-1} \Delta_\mu) \]](form_21.png)
Definition at line 133 of file data_utils.h.
◆ productIntegralTwoGaussians() [2/2]
| T mrpt::math::productIntegralTwoGaussians | ( | const std::vector< T > & | mean_diffs, |
| const CMatrixFixedNumeric< T, DIM, DIM > & | COV1, | ||
| const CMatrixFixedNumeric< T, DIM, DIM > & | COV2 | ||
| ) |
Computes the integral of the product of two Gaussians, with means separated by "mean_diffs" and covariances "COV1" and "COV2".
![\[ D = \frac{1}{(2 \pi)^{0.5 N} \sqrt{} } \exp( \Delta_\mu^\top (\Sigma_1 + \Sigma_2)^{-1} \Delta_\mu) \]](form_22.png)
Definition at line 156 of file data_utils.h.
References ASSERT_, M_2PI, and mrpt::math::UNINITIALIZED_MATRIX.
◆ weightedHistogram()
| void mrpt::math::weightedHistogram | ( | const VECTORLIKE1 & | values, |
| const VECTORLIKE1 & | weights, | ||
| float | binWidth, | ||
| VECTORLIKE2 & | out_binCenters, | ||
| VECTORLIKE2 & | out_binValues | ||
| ) |
Computes the weighted histogram for a vector of values and their corresponding weights.
- Parameters
-
values [IN] The N values weights [IN] The weights for the corresponding N values (don't need to be normalized) binWidth [IN] The desired width of the bins out_binCenters [OUT] The centers of the M bins generated to cover from the minimum to the maximum value of "values" with the given "binWidth" out_binValues [OUT] The ratio of values at each given bin, such as the whole vector sums up the unity.
- See also
- weightedHistogramLog
Definition at line 369 of file data_utils.h.
References ASSERT_, ASSERTDEB_, mrpt::math::maximum(), mrpt::math::minimum(), MRPT_END, MRPT_START, and mrpt::utils::round().
◆ weightedHistogramLog()
| void mrpt::math::weightedHistogramLog | ( | const VECTORLIKE1 & | values, |
| const VECTORLIKE1 & | log_weights, | ||
| float | binWidth, | ||
| VECTORLIKE2 & | out_binCenters, | ||
| VECTORLIKE2 & | out_binValues | ||
| ) |
Computes the weighted histogram for a vector of values and their corresponding log-weights.
- Parameters
-
values [IN] The N values weights [IN] The log-weights for the corresponding N values (don't need to be normalized) binWidth [IN] The desired width of the bins out_binCenters [OUT] The centers of the M bins generated to cover from the minimum to the maximum value of "values" with the given "binWidth" out_binValues [OUT] The ratio of values at each given bin, such as the whole vector sums up the unity.
- See also
- weightedHistogram
Definition at line 423 of file data_utils.h.
References ASSERT_, ASSERTDEB_, mrpt::math::maximum(), mrpt::math::minimum(), MRPT_END, MRPT_START, and mrpt::utils::round().